The dynamics of the net are described perfectly by the state transition table or diagram. However, greater insight may be derived if we can express this in terms of an energy function and, using this formulation, it is possible to show that stable states will always be reached in such a net.
Consider two nodes in the net which are connected by a positive
weight and where j is currently outputting a `0' while i
is outputting a `1'.
two nodes in conflict
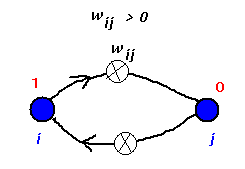
If j were given the chance to update or fire, the contribution to its activation from i is positive and this may well serve to bring j's activation above threshold and make it output a `1'. A similar situation would prevail if the initial output states of the two nodes had been reversed since the connection is symmetric. If, on the other hand, both units are `on' they are reinforcing each other's current output. The weight may therefore be thought of as fixing a constraint between i and j that tends to make them both take on the value `1'. A negative weight would tend to enforce opposite outputs. One way of viewing these networks is therefore as constraint satisfaction nets.
This idea may be captured quantitatively in the form of a suitable energy function. Define
The values that take are given in the table below
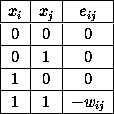
If the weight is positive then the last entry is negative and is the
lowest value in the table. If is regarded as the `energy'
of the pair ij then the lowest energy occurs when both units
are on which is consistent with the arguments above. If the weight
is negative, the `11' state is the highest energy state and is not
favoured. The energy of the net is found by summing over all pairs
of nodes
This may be written
Since the sum includes each pair twice (as and
) and
.
It is now instructive to see what the change in energy is when a node fires. Suppose node k is chosen to be updated. Write the energy E by singling out the terms involving this node.
Now, because , the last two sums may be combined
For ease of notation, denote the first sum by S and take the
outside the sum since it is constant throughout, then
but the sum here is just the activation of the kth node so that
Let the energy after k has updated be and the
new output be
. Then
Denote the change in energy by
and the change in
output
by
, then subtracting (7)
from (8)
There are now two cases to consider
state transitions to stable state
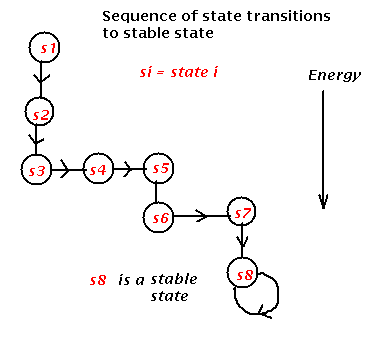
In the example given above, all state have zero energy except for state 5 which has energy 2, and the stable states 3 and 6 which have energy -1.