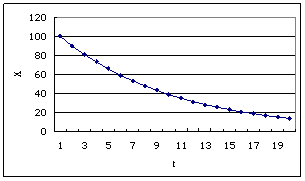
X : 系統狀態

t : 離散時間

f : 函式

系統動態模擬：迭代

Xt+1= rXt

迭代結果：

X0 : 系統初始狀態
X1 =rX0
X2 =rX1=r²X0
X3 =rX2=r²X1=r³X0
…………

1.模擬以下線性系統

   Xt+1= 0.9Xt

設初始條件X0= 100

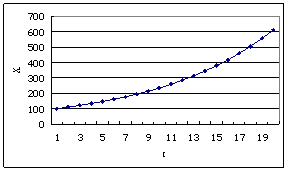
再將系統改為

   Xt+1= 1.1Xt

重新模擬。

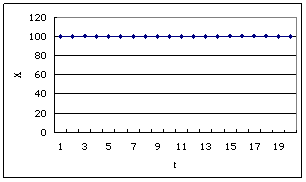
如果將系統改為

   Xt+1= 1.0Xt

　

   Xt+1= -1.0Xt

觀察系統行為。

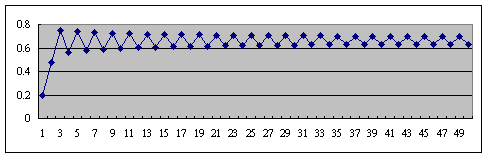
2. 模擬非線性系統

    Xt+1= rXt (1-Xt)

請模擬

r=0.15及X0=0.1

和

r=2.95及X0=0.7

兩種動態系統行為

　

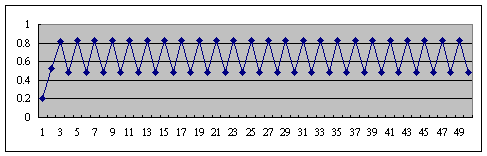
3. 模擬非線性系統的混沌現象

使用第2題的非線性方程式

系統初始狀態X0設定為0.2

變化r, 分別令 r=3.0, 3.3, 3.6, 3.9, 4.0讓系統迭代50次，分別畫出其曲線如

r=3.0

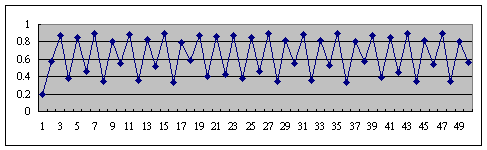
r=3.3

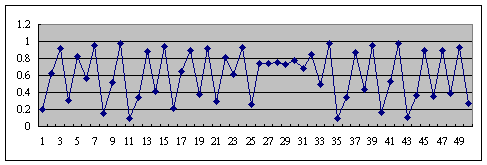
r=3.6

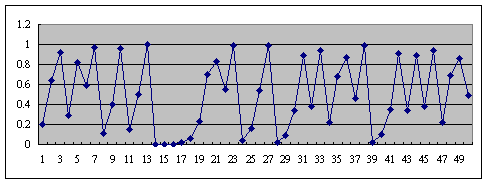
r=3.9

r=4.0