2. Hopfield Neural Network

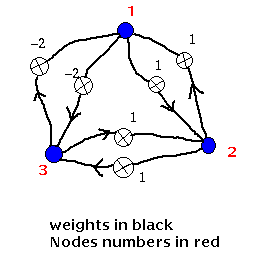
The Hopfield neural network is a simple artificial network which is able to store certain memories or patterns in a manner rather similar to the brain - the full pattern can be recovered if the network is presented with only partial information. Furthermore there is a degree of stability in the system - if just a few of the connections between nodes (neurons) are severed, the recalled memory is not too badly corrupted - the network can respond with a "best guess". Of course, a similar phenomenon is observed with the brain - during an average lifetime many neurons will die but we do not suffer a catastrophic loss of individual memories - our brains are quite robust in this respect (by the time we die we may have lost 20 percent of our original neurons).

The nodes in the network are vast simplifications of real neurons - they can only exist in one of two possible "states" - firing or not firing. Every node is connected to every other node with some strength. At any instant of time a node will change its state (i.e start or stop firing) depending on the inputs it receives from the other nodes.

If we start the system off with a any general pattern of firing and non-firing nodes then this pattern will in general change with time. To see this think of starting the network with just one firing node. This will send a signal to all the other nodes via its connections so that a short time later some of these other nodes will fire. These new firing nodes will then excite others after a further short time interval and a whole cascade of different firing patterns will occur. One might imagine that the firing pattern of the network would change in a complicated perhaps random way with time. The crucial property of the Hopfield network which renders it useful for simulating memory recall is the following: we are guaranteed that the pattern will settle down after a long enough time to some fixed pattern. Certain nodes will be always "on" and others "off". Furthermore, it is possible to arrange that these stable firing patterns of the network correspond to the desired memories we wish to store!

The smart thing about the Hopfield network is that there exists a rather simple way of setting up the connections between nodes in such a way that any desired set of patterns can be made "stable firing patterns". Thus any set of memories can be burned into the network at the beginning. Then if we kick the network off with any old set of node activity we are guaranteed that a "memory" will be recalled. Not too surprisingly, the memory that is recalled is the one which is "closest" to the starting pattern. In other words, we can give the network a corrupted image or memory and the network will "all by itself" try to reconstruct the perfect image. Of course, if the input image is sufficiently poor, it may recall the incorrect memory - the network can become "confused" - just like the human brain. We know that when we try to remember someone's telephone number we will sometimes produce the wrong one! Notice also that the network is reasonably robust - if we change a few connection strengths just a little the recalled images are "roughly right". We don't lose any of the images completely.

3 node Hopfield net

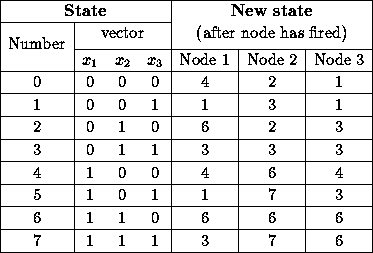
Every node is connected to every other node (but not to itself) and the connection strengths or weights are symmetric in that the weight from node i to node j is the same as that from node j to node i. That is, , and for all . Notice that the flow of information in this net is not in a single direction as it has been in the nets dealt with so far. It is possible for information to flow from a node back to itself via other nodes. That is, there is feedback in the network and so they are known as feedback or recurrent nets as opposed to feedforward nets which were the subject of the Backpropagation algorithm.

The state of the net at any time is given by the vector of the node outputs . Suppose we now start this net in some initial state and choose a node at random and let it update its output or `fire'. That is, it evaluates its activation in the normal way and outputs a `1' if this is greater than or equal to zero and a `0' otherwise. The net now finds itself either in the same state as it started in, or in a new state which is at Hamming distance one from the old. We now choose a new node at random to fire and continue in this way over many steps. What will the behaviour of the net be? For each state, we may evaluate the next state given each of the three nodes fires. This gives the following table.

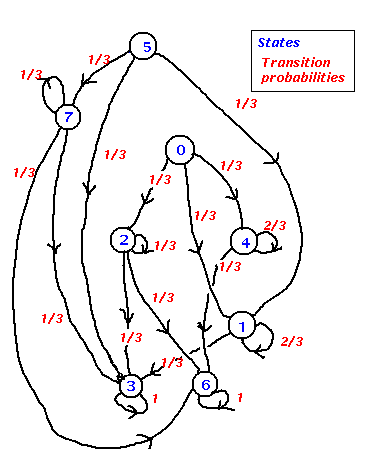
This information may be represented in graphical form as a state transition diagram.

state transition diagram for 3 node net

States are represented by the circles with their associated state number. Directed arcs represent possible transitions between states and the number alongside each arc is the probability that each transition will take place. The states have been arranged in such a way that transitions tend to take place down the diagram; this will be shown to reflect the way the system decreases its energy. The important thing to notice at this stage is that, no matter where we start in the diagram, the net will eventually find itself in one of the states `3' or `6'. These reenter themselves with probability 1. That is they are stable states - once the net finds itself in one of these it stays there. The state vectors for `3' and `6' are (0,1,1) and (1,1,0) respectively and so these are the `memories' stored by the net.