|
ADAPTIVE K-MEANS CLUSTERING
ALGORITHM
- One cluster center is updated
every time an input vector
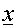 is chosen at random from the input data
set. is chosen at random from the input data
set.
- The cluster nearest to
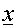 has
its position updated using has
its position updated using 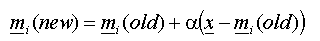 where where 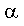 is the
learning rate. is the
learning rate.
- Notice how the cluster centre
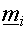 is moved closer to
is moved closer to 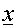 because this equation minimizes the error vector because this equation minimizes the error vector 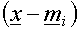 . .
- This algorithm is typically
used for clustering the input vectors in real-time as they are acquired
sequentially.
- Note that batch K-means
clustering algorithm is much better than the adaptive version because it
has a stopping criterion and does not require a learning rate
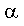 . .
- The results of applying the
adaptive clustering algorithm to the example shown in the previous
lecture is presented below, using a learning rate of 0.1. The
diamond shaped points are the cluster centers using this adaptive
algorithm.
RADIAL
BASIS FUNCTION (RBF) NETWORKS
Using a clustering procedure
(K-means batch or adaptive) creates a set of cluster centers 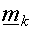 , which
can be thought of as the average input vector for the
kth cluster, or more appropriately, as the prototype
vector for that cluster. , which
can be thought of as the average input vector for the
kth cluster, or more appropriately, as the prototype
vector for that cluster.
- The output of a neuron in the
output layer of an RBF network
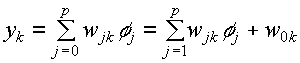 since the bias
output since the bias
output 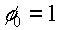 . .
- The basis function
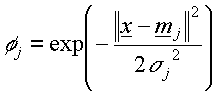
where 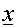 is the input vector is the input vector
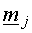 is the
jth prototype vector is the
jth prototype vector
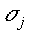 is the width of
the Gaussian of that prototype or cluster centre is the width of
the Gaussian of that prototype or cluster centre
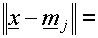 Euclidean
distance between Euclidean
distance between 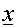 and and 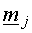
Hence from
the basis function 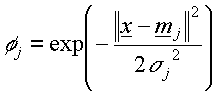 , we see that the output , we see that the output 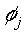 only has a
significant value if the Euclidean distance between the input vector only has a
significant value if the Euclidean distance between the input vector 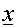 and a
prototype vector and a
prototype vector 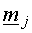 is within a radius
2 is within a radius
2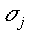 around
around 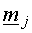 . . |
![]()